 A free C++/Python discrete Element workbench
A free C++/Python discrete Element workbench
Welcome to GranOO, a robust and versatile workbench to build 3D dynamic simulations based on the Discrete Element Method (DEM) distributed under the free GPLv3 license.
GranOO is not a software, GranOO is a collection of C++ libraries and tools that help users for building a specific DEM simulation. Python bindings have been recently released to improve user experience.
GranOO is modular ! You can build your own simulation by plugin specific treatments in any order. This design is perfectly adapted to conduct high level simulations for research activities with DEM.
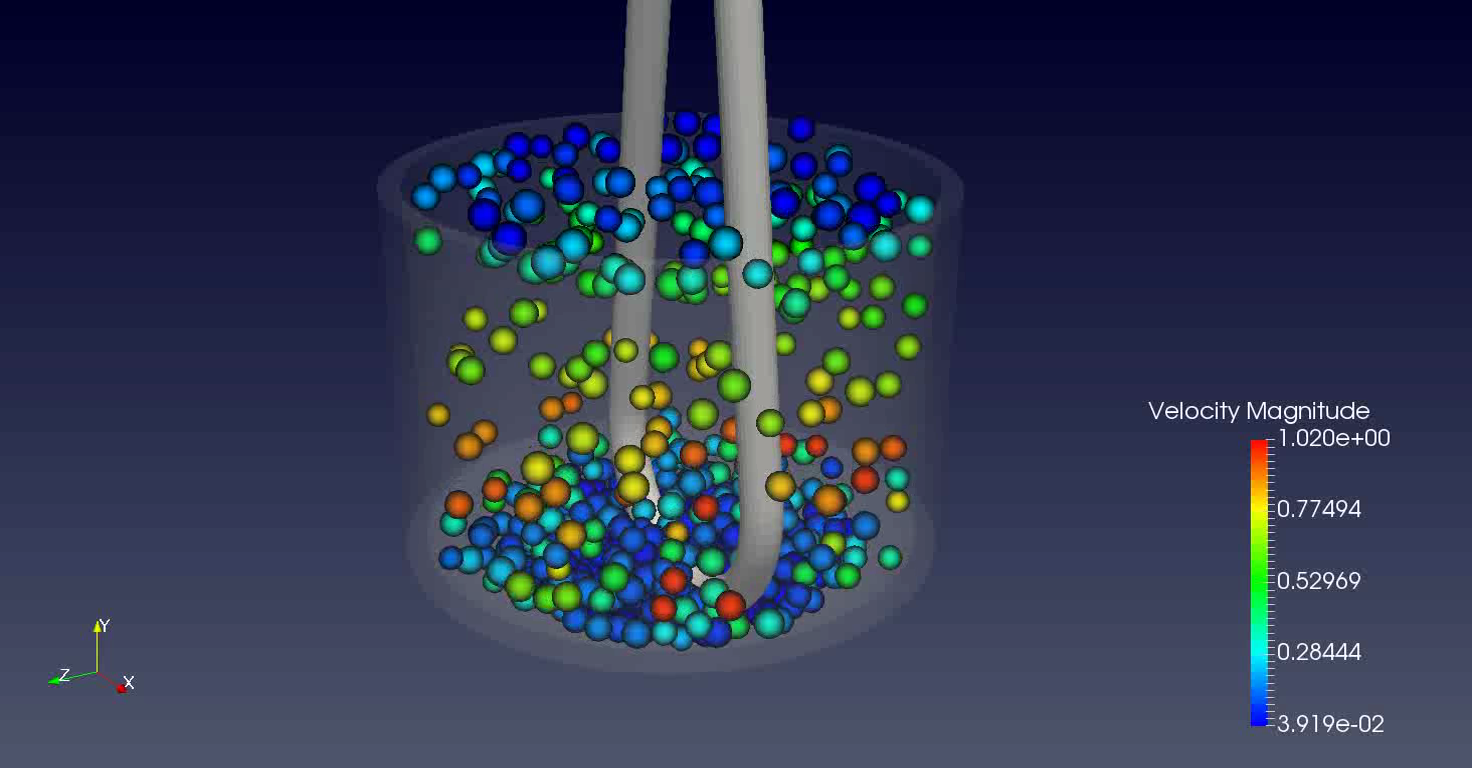

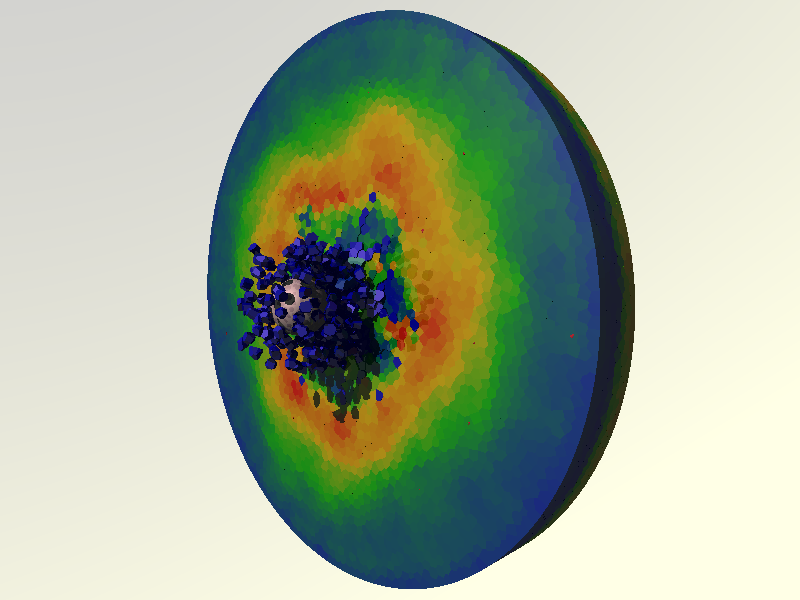


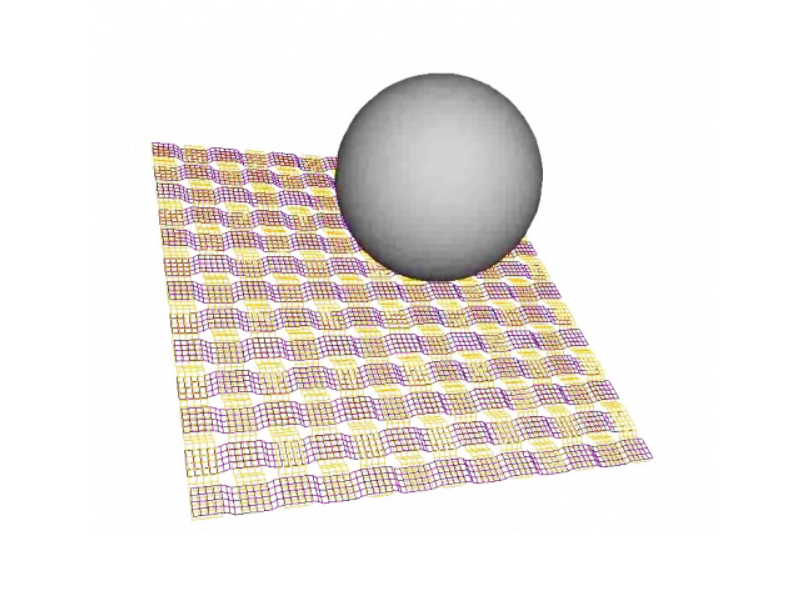


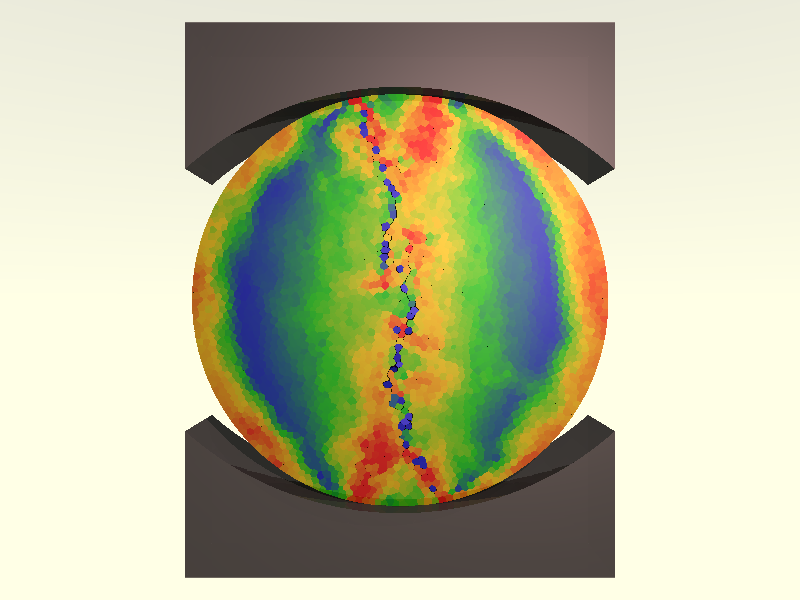






GranOO is a dynamic explicit DEM code specialized in modeling continuous materials with high amount of discontinuities. GranOO embeds mechanical, thermal and electrical models in order to perform multi-physic simulation. GranOO can also be used for granular simulation with arbitrary shapes and state-of-art contact detection processing.
GranOO implements regular contact laws, different kind of joints (for continuous modeling) and several explicit time schemes. This configuration is well adapted to solve multi-physical discontinuous dynamic problems like wear, multi-fracturation, impact…
GranOO does not make any assumption on your simulation. Each family of simulation requires to build a kind of application. In this process, you can both use Python or C++. For beginners, we recommend Python. You can deploy your simulation and set it through easy-to-read XML input files that describe the main steps of your simulation.
GranOO is not a commercial software. We are a small developer team and we do not have any time for developing nice and smart graphical interfaces. We choose to focus on the essential : models and physics. Since the 2.0 version, GranOO can use python as an easy interface language. So if you are ready to program with Python or C++, GranOO may be yours !
The different simulation steps are described through C++ or Python plugins. GranOO embeds a huge collection of plugins that you can reuse at your convenience. However, if your simulation requires specific treatments, you can write your own plugins. This is easy, you just have to follow and fill the provided template files.
The example below shows the XML input file related to the granular rain example.
<GranOO TotIteration="20000" TimeStep="2e-5" OutDir="Results"/>
<PreProcessing>
<PlugIn Id="_NewSupportShape" Type="Box" DimX="1." DimY="0.25" DimZ="1."/>
</PreProcessing>
<Processing> <!-- The time loop -->
<PlugIn Id="AddElement"/>
<PlugIn Id="_ClearLoad"/>
<PlugIn Id="_ApplyGravity" X="0." Y="-10." Z="0."/>
<PlugIn Id="_ManageCollision" Between="DiscreteElement/SupportShape" ...some options here.../>
<PlugIn Id="_ManageCollision" Between="DiscreteElement/DiscreteElement" ..some options here.../>
<PlugIn Id="_IntegrateAcceleration" Linear="Yes" Angular="Yes"/>
</Processing>
</GranOO>Please visit our installation instructions in order to install GranOO or go below to get a list of rigorous scientific productions related to this project.
Marchais, K., Girardot, J., Metton, C., Iordanoff, I. (2021).
A 3D DEM simulation to study the influence of material and process parameters on spreading of metallic powder in additive manufacturing.
Computational Particle Mechanics.
Girardot, J., Prulière, E. (2021).
Elastic calibration of a discrete domain using a proper generalized decomposition.
Computational Particle Mechanics.
Ratsimba, A and Zerrouki, A and Tessier-Doyen, N and Nait-Ali, B and André, D and Duport, P and Neveu, A and Tripathi, N and Francqui, F and Delaizir, G (2020).
Densification behaviour and three-dimensional printing of Y2O3 ceramic powder by selective laser sintering.
Ceramics International.
Lemesle, J., Hubert, C. and Bigerelle, M. (2020).
Numerical Study of the Toughness of Complex Metal Matrix Composite Topologies.
Applied Sciences, 10(18), 6250.
Moreira, M. H., Cunha, T. M., Campos, M. G. G., Santos, M. F., Santos Jr, T., André, D., & Pandolfelli, V. C. (2020).
Discrete element modeling—A promising method for refractory microstructure design.
American Ceramic Society Bulletin.
Nguyen, V.D.X., Tieu, A.K., André, D. et al (2019).
Discrete element method using cohesive plastic beam for modeling elasto-plastic deformation of ductile materials.
Computational Particle Mechanics.
Damien André, Jérémie Girardot and Cédric Hubert (2019).
A novel DEM approach for modeling brittle elastic media based on distinct lattice spring model.
Computer Methods in Applied Mechanics and Engineering.
Truong-Thi Nguyen, Damien André and Marc Huger (2019).
Analytic laws for direct calibration of discrete element modeling of brittle elastic media using cohesive beam model.
Computational Particle Mechanics.
Curti, R., Girardon, S., Pot, G., & Lorong, P. (2018).
How to model orthotropic materials by the discrete element method (DEM): random sphere packing or regular cubic arrangement ?
Computational Particle Mechanics, 1-11.
Coré, A., Kopp, J. B., Girardot, J., & Viot, P. (2018),
Dynamic energy release rate evaluation of rapid crack propagation in discrete element analysis,
International Journal of Fracture, 214(1), 17-28.
del Sorbo, P., Girardot, J., Dau, F., & Iordanoff, I. (2018).
Numerical investigations on a yarn structure at the microscale towards scale transition.
Composite Structures, 183, 489-498.
Jebahi, M., Dau, F., Iordanoff, I., & Guin, J. P. (2017).
Virial stress–based model to simulate the silica glass densification with the discrete element method.
International Journal for Numerical Methods in Engineering, 112(13), 1909-1925.
André, D., Levraut, B., Tessier-Doyen, N. & Huger, M. (2017),
A discrete element thermo-mechanical modelling of diffuse damage induced by thermal expansion mismatch of two-phase materials,
Computer Methods in Applied Mechanics and Engineering, 318, 898-916.
C. Hubert, D. André, L. Dubar, I. Iordanoff, J.L. Charles, (2017),
Simulation of continuum electrical conduction and Joule heating using DEM domains,
International Journal for Numerical Methods in Engineering, 110, Issue 9, pp. 862-877 (2017)
Girardot, J., & Dau, F. (2016),
A mesoscopic model using the discrete element method for impacts on dry fabrics.
Matériaux & Techniques, 104(4), 408
Jebahi, M., Dau, F., Charles, J. L., & Iordanoff, I. (2016).
Multiscale modeling of complex dynamic problems: an overview and recent developments.
Archives of Computational Methods in Engineering, 23(1), 101-138.
L. Maheo, F. Dau, D. André, J.L. Charles, I. Iordanoff, (2015),
A promising way to model cracks in composite using Discrete Element Method,
Composites Part B: Engineering, Vol. 71, pp. 193-202, 2015
André D., Charles J.L., Iordanoff I., Néauport J., (2014),
The GranOO workbench, a new tool for developing discrete element simulations and its application to tribological problems,
Advances in Engineering Software, Vol. 74, pp. 40-48, 2014
Goupil A., Iordanoff I., Charles J.L., Rinchet A., (2013),
Modelling of Polishing Tools for High Spatial Frequency Defect Correction on Aspherical Surfaces,
Key Engineering Materials, Vol. 554-557, pp. 1232-1241, 2013
Jebahi M., Charles J.L., Dau F., Illoul L., Iordanoff I., (2013),
3D coupling approach between discrete and continuum models for dynamic simulations (DEM–CNEM),
Computer Methods in Applied Mechanics and Engineering, Vol. 255, pp. 196-209, 2013
Terreros I., Iordanoff I., Charles J.L., (2013),
Simulation of continuum heat conduction using DEM domains,
Computational Materials Science, Vol. 69, pp. 46-52, 2013
Pennec F., Alzina A., Tessier-Doyen N., Naït-ali B., Mati-Baouche N., De Baynast H., Smith D.S., (2013),
A combined finite-discrete element method for calculating the effective thermal conductivity of bio-aggregates based materials,
International Journal of Heat and Mass Transfer, Vol. 60, pp. 274-283, 2013
preprint version
Jebahi M., André D., Dau F., Charles J.L., Iordanoff I., (2013),
Simulation of Vickers indentation of silica glass,
Journal of Non-Crystalline Solids, Vol. 378, pp. 15-24, 2013
André D., Jebahi M., Iordanoff I., Charles J.L., Néauport J., (2013),
Using the discrete element method to simulate brittle fracture in the indentation of a silica glass with a blunt indenter,
Computer Methods in Applied Mechanics and Engineering, Vol. 265, pp. 136-147, 2013
André D., Iordanoff I., Charles J.L., Néauport J., (2012),
Discrete element method to simulate continuous material by using the cohesive beam model,
Computer Methods in Applied Mechanics and Engineering, Vol. 213-216, pp. 113-125, 2012
Duplessis-Kergomard Y., Dau F., Iordanoff I., (2011)
Implementation of a Discrete Element Method for the space-time modeling of loading in the case of a soft shock: qualitative approach,
International Journal of Computations and Modelling, vol.1, no.2, 39-72, 2011
Mohamed Jebahi, Damien André, Inigo Terreros, Ivan Iordanoff, (2015),
Discrete Element Method to Model 3D Continuous Materials,
ISTE, Wiley, Numerical Methods in engineering series, 2015
Mohamed Jebahi, Frédéric Dau, Jean-Luc Charles, Ivan Iordanoff, (2015),
Discrete-Continuum Coupling Method to Simulate Highly Dynamic Multi-Scale Problems,
ISTE, Wiley, Numerical Methods in engineering series, 2015
Damien André, Jean-Luc Charles, Ivan Iordanoff, (2015),
3D Discrete Element Workbench for Highly Dynamic Thermo-Mechanical Analysis : GranOO,
ISTE, Wiley, Numerical Methods in engineering series, 2015
Damien André, Jean-luc Charles, Jérémie Girardot, Cédric Hubert, Ivan Iordanoff, Iñigo Terreros and a lot of contributors !
To contact us please send an email to team@granoo.org